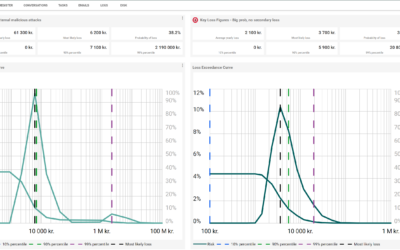
When you assess IT-risk, you want to understand the probability of certain risk scenarios together with their potentiel loss in monetary values. This is where quantitative solutions come handy.
- How does a quantitative risk assessment work?
- How do I get started with quantitative risk assessment?
We have created a step-by-step guide here.
There is a whole spectrum of quantitative solutions, from the very simple to the very advanced. In this article we choose to introduce you to the simplest probabilistic model. It’s to some degree a direct one-one substitution of the common risk matrix.
A SIMPLE PROBABILISTIC MODEL
Many risk managers are familiar with the qualitative methods including the risk matrix and verbal scales. We have discussed this in the article: Risikomatricer til it-risikovurderinger – den mest anvendte metode, der ikke virker.
For an estimate we will use the same source as with the qualitative methods – a subject matter expert (SME) in the organization. Just as an expert assesses likelihood and impact on the conventional risk matrix, he can simply assess these values using meaningful quantities. We propose that instead of using the scales such as high, medium, low, or 1 to 5, experts learn how to subjectively assess the actual quantities behind those scales – which is, probability and monetary impact.
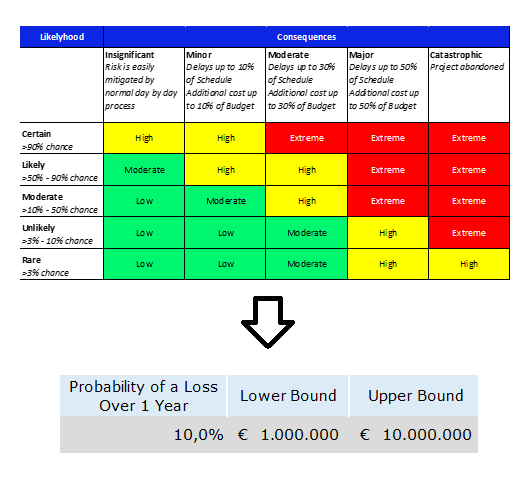
To start with, instead of rating likelihood on a scale of 1 to 5 or “low” to “high” (Example: “likelihood of X is a 2” or “likelihood of X is moderate”), we suggest estimating the probability of the event occurring in a given period of time (e.g.,1 year) “Event X has a 10 percent chance of occurring in the next 12 months.” (“Probability of a Loss Over 1 Year” column)
Next, instead of rating impact on a scale of 1 to 5 or “low” to “high” (Example: “Impact of X is a 2” or “impact of X is moderate”), we suggest to estimate a 90 percent confidence interval for a monetized loss, “If event X occurs, there is a 90 percent chance the loss will be between € 1 million and € 10 million.” (Which will be “Lower Bound” column and “Upper Bound” column accordingly.)
Then, instead of plotting likelihood and impact scores on a risk matrix, as we already have the quantitative likelihood and impact, use them to generate a loss exceedance curve – a quantitative approach to expressing risk – using a Monte Carlo simulation done in a “Loss Exceedance Curve” spreadsheet.
Finally, instead of dividing the risk matrix into risk categories such as low, medium, high or green, yellow, red and guessing whether you should do something and what you should do, compare the loss exceedance curve to a risk appetite curve (See article: Risikoappetit – hvorfor og hvordan?) and prioritize actions based on return on mitigation.
The method proposed – a Simple Probabilistic Model – is really just another expression of your current state of uncertainty. We are stating our current uncertainty about it in a way that enables us to update this uncertainty with new information.
Now let’s look at the process and put together the pieces of this approach, starting with how we come up with subjective estimates of probability.
THE PROCESS
To try the quantitative process as described in the steps below, we have developed a simple Excel template. To get the template just ask for it at info@aci.dk
We suggest that you open the Excel file and use it together with the following guidelines.
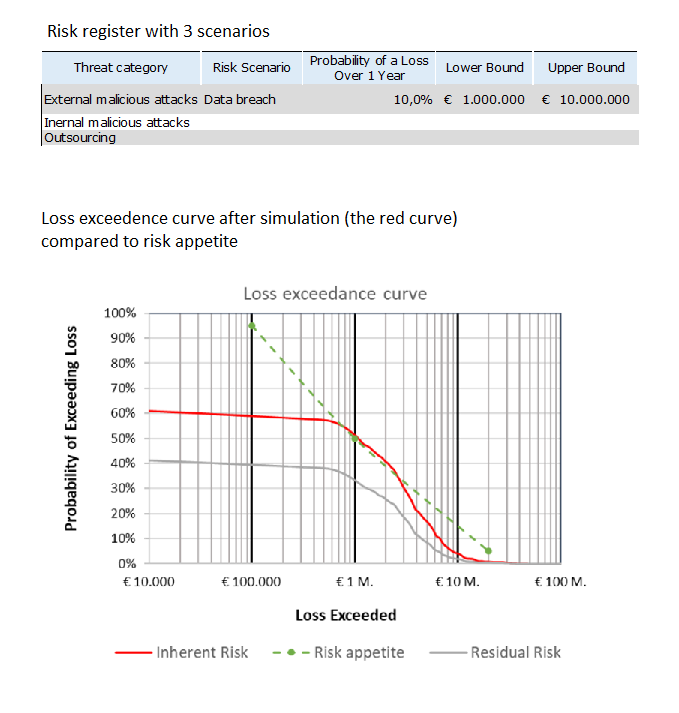
1. Define your Risk Scenarios
There are different options for categorizing risk scenarios, but for now let’s just categorize them according to some threat categories given in “Threat category” column of the “Risk Estimates” spreadsheet.
-
- For each dot on your risk matrix, create one row for input in the Excel spreadsheet. Whatever the name of that threat is, type that name in the “Threat category” column. This helps you to categorize all the risks.
- Write a risk scenario in the “Risk Scenario” column. See article: Hvordan man skriver et godt risikoscenarie? For now, we write very simple scenarios.
2. DEFINE PERIOD
Define a specific period over which the risk events could materialize. It could be one year; a decade or whatever time frame makes sense – just use it consistently for all the risks. We use 1 year period in our spreadsheet.
3. ASSIGN PROBABILITY
For each risk scenario, subjectively assign a probability (0 percent to 100 percent) that the stated event will occur in the specified time (e.g., “There is a 10 percent chance a data breach of system X will occur in the next twelve months”).
4. ASSIGN MONETARY LOSS
For each risk, subjectively assign a range for a monetary loss if such an event occurs as a 90 percent confidence interval. In other words, this is a range wide enough that you are 90 percent certain that the actual loss will be within the stated range (e.g., if there is a data breach in application X, then it is 90 percent likely that there will be a loss equal to somewhere between $1 million and $10 million). Don’t try to capture the most extreme outcomes possible. (See article: Kunsten at kunne afgive et 90% konfidensinterval ved hjælp af dekomponering og kalibrering)
Get the estimates from multiple experts if possible. Once we have recorded the likelihood and 90 percent confidence interval of losses for each risk scenario in the table, we are ready for the next step.
5. RUN SIMULATION
Run simulation to add up the risks. The result will be the loss exceedance curve with risk appetite curve and expected inherent loss in monetary values inclusive expected residual loss.
This exercise with basic steps helps us to generate the expected loss and compare loss exceedance curve to the risk appetite. This helps us to prioritize actions based on return on mitigation.
Conclusion
We’ve looked at a simple probabilistic model for risk assessments. What have we learned?
We have substituted each element of the common risk matrix with a method that uses explicit probabilities:
- Instead of rating likelihood on a scale of 1 to 5 or “low” to “high” we estimated the probability of the event occurring in a given period (e.g.,1 year).
- Instead of rating impact on a scale of 1 to 5 or “low” to “high” we estimated a 90 percent confidence interval for a monetized loss.
We have used a SME (subject matter expert) in cybersecurity to estimate various risks. We:
- defined risk scenarios.
- defined a specific time-period over which the risk events could materialize.
- assigned a probability and the 90 percent confidence interval of the losses in monetary value for each risk scenario.
We have generated a loss exceedance curve – a quantitative approach to expressing risk – using a Monte Carlo simulation.
We have prepared graphs and figures that, in turn, helps us to:
- Compare loss exceedance curve to the risk appetite.
- Prioritize actions based on return on mitigation.
There you are. Your first quantitative risk assessment based on simulation. It goes further in depths of complexity, but that’s basically just developments to this simple model. We’ll continue to discuss these methods and come up with advice and tools for those who wants to get start quantifying.
So, stay tuned.